quadratique

quadratique [ k(w)adratik ] adj.

• 1751; du lat. quadratus « carré »

1 ♦ Math. Qui est du second degré, élevé au carré. ⇒ rectangle (2^o). Moyenne quadratique de n nombres : racine carrée du quotient par n de la somme de leurs carrés.

2 ♦ (1859) Minér. Se dit d'un système cristallin caractérisé par trois axes de longueurs égales faisant entre eux des angles droits; et d'un minéral qui appartient à ce système. Cristal quadratique.

● quadratique adjectif Équation quadratique, équation du second degré. Forme quadratique sur un K-espace vectoriel (K corps commutatif) E, application q de E dans K vérifiant ● quadratique (expressions) adjectif Équation quadratique, équation du second degré. Forme quadratique sur un K-espace vectoriel (K corps commutatif) E, application q de E dans K vérifiant

quadratique

adj.

d1./d MATH Qui est du second degré.

|| Moyenne quadratique de deux nombres: V. moyenne.

d2./d MINER Système quadratique ou tétragonal: système de la cristallographie auquel appartiennent les cristaux caractérisés par les éléments de symétrie du prisme droit à base carrée.

⇒QUADRATIQUE, adj.

A. — MATH. Qui est élevé au carré; qui suit une loi du carré. Synon. du second degré. Moyenne quadratique. Il faut compter comme une des contributions les plus importantes des Babyloniens le fait qu'ils aient su ramener la résolution des équations quadratiques et bicarrées à une seule opération algébrique nouvelle, l'extraction des racines carrées (BOURBAKI, Hist. math., 1960, p. 92). Une fonction quadratique s'écrit y = f(x²). Elle s'exprime analytiquement par une parabole (BUREAU 1972).

♦ Forme quadratique. ,,Polynôme homogène de degré 2, le nombre de variables pouvant être quelconque`` (Lar. encyclop.). En théorie des nombres, une forme quadratique est une expression homogène du second degré par rapport à des variables X, Y, Z, ..., T, ne prenant que des valeurs entières relatives et dont les coefficients sont eux-mêmes des entiers relatifs (Hist. gén. sc., t. 3, vol. 1, 1961, p. 72).

B. — CRISTALLOGR., MINÉR. [En parlant d'un des six systèmes cristallins] Caractérisé par les éléments de symétrie du prisme droit à base carrée (d'apr. GRAND. 1962). Système quadratique.

— [En parlant d'un corps] Qui appartient à ce système. L'étain natif est très rare. Quadratique à l'état naturel et rhombique en cristaux artificiels (...), il a été trouvé en grains roulés, seul ou associé à l'or (LAPPARENT, Minér., 1899, p. 581).

Prononc.:[k(w)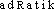]. V. quadr(i)-. Étymol. et Hist. 1. 1765 math. équation quadratique (Encyclop.); 1842 « relatif au carré » (Ac. Compl.); 2. 1859 cristallogr. (BOUILLET); 1932 système quadratique « système de cristaux ayant la symétrie du prisme droit à base carrée » (Lar. 20^e). Dér. sav. du lat. quadratus (v. carré); suff. -ique.

quadratique [kadʀatik; kwadʀatik] adj.

ÉTYM. 1765; dér. sav. du lat. quadratus « carré ». → Cadrat.

❖

♦ Didactique.

1 Math. Qui est du second degré élevé au carré. ⇒ Rectangle. || Équation quadratique : équation du second degré. || Moyenne quadratique de n nombres.

2 (1869). Sc. nat. || En cristallographie, Système quadratique : un des six systèmes cristallins, caractérisé par trois axes de longueurs égales faisant entre eux des angles droits. Par ext. Qui appartient à ce système. || Cristal quadratique. || L'étain est quadratique.

❖

COMP. Biquadratique.

Encyclopédie Universelle. 2012.